EFFECT OF FEEDBACK ON STABILITY
Stability is a notion that describes whether the system will be able to follow the input command, that is, be useful in general. In a non-rigorous manner, a system is said to be unstable if its output is out of control. To investigate the effect of feedback on stability, from the below above. If GH = – 1, the output of the system is infinite for any finite input, and the system is said to be unstable. Therefore, we may state that feedback can cause a system that is originally stable to become unstable. Certainly, feedback is a double-edged sword; when it is improperly used, it can be harmful. It should be pointed out, however, that we are only dealing with the static case here, and in general, GH = — 1 is not the only condition for instability. It can be demonstrated that one of the advantages of incorporating feedback is that it can stabilize an unstable system If we introduce another feedback loop through a negative Feedback gain of F, as shown in Fig. given below, the input-output relation of the overall system is

It is apparent that although the properties of G and H are such that the inner-loop feedback system is unstable, because GH = -1, the overall system can be stable by properly selecting the outer-loop feedback gain F. In practice, GH is a function of frequency, and the stability condition of the closed-loop system depends on the magnitude and phase of GH. The bottom line is that feedback can improve stability or be harmful to stability if it is not properly applied. Sensitivity considerations often are important in the design of control systems. Because all physical elements have properties that change with the environment and age, we cannot always consider the parameters of a control system to be completely stationary over the entire operating life of the system. For instance, the winding resistance of an electric motor changes as the temperature of the motor rises during operation. Control systems with electric components may not operate normally when first turned on because of the still changing system parameters during warm-up. This phenomenon is sometimes called “morning sickness.” Most duplicating machines have a warm-up period during which time operation is blocked out when first turned on. In general, a good control system should be very insensitive to parameter variations but sensitive to the input commands. We shall investigate what effect feedback has on sensitivity to parameter variations. We consider G to be a gain parameter that may vary. The sensitivity of the gain of the overall system M to the variation in G is defined as
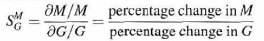
Where dM denotes the incremental change in M due to the incremental change in G, or dG. The sensitivity function is written
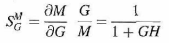
This relation shows that if GH is a positive constant, the magnitude of the sensitivity function can be made arbitrarily small by increasing GH, provided that the system remains stable. It is apparent that, in an open-loop system, the gain of the system will respond in a one-to-one fashion to the variation in G. Again, in practice, GH is a function of frequency; the magnitude of 1+GH may be less than unity over some frequency ranges, so feedback could be harmful to the sensitivity to parameter variations in certain cases. In general, the sensitivity of the system gain of a feedback system to parameter variations depends on where the parameter is located. The reader can derive the sensitivity of the system in Fig due to the variation of H.
Related Topic – click here
- What Is A Diode? Working Principle & Types | Different Types Of Resistors
- What Is Synchronous Speed? | Types & Advantages Of DC Motors
- Working Principle Of Linear Variable Differential Transformer | Construction & Piezoelectric Transducers
- Three-Phase Induction Motor | 3-Phase Induction Motor Principle
- Introduction To Electrical Transformer | Definition, Construction & Parts Of A Transformer | Types Of Transformers
- DC Generator | Principle Of Operation, Construction, Types Of Generators & Application
- What Is DC Motor? | Principle Of DC Motor & Types Of DC Motors
- Diode-Circuits |Diode Convention, Transformer Rectifier & Objective Questions With Answer

