A wetted wall column is used to study the distillation, gas absorption, and vaporization operation of various chemical systems, to obtain data and correlation between components present in different phases which exist in equilibrium conditions during the operation. The experiments of wetted wall columns provide data for the design of separation operations.
The aim of the wetted wall column experiment
Evaluation of Mass Transfer Coefficient in a wetted wall column
Objective: The rates of diffusion into gases flowing through pipes are studied in wetted wall columns.
Principle/Theory:
A thin film of liquid falling down the inside of a vertical pipe through which the gas flows constitutes a wetted wall column. Wetted wall columns have been used as absorbers of Hydrochloric acid, Ammonia, Acetone, Benzene, and other volatile liquids. They have also been studied for theoretical studies for mass transfer because the interfacial surface between the phases is kept under control and is measurable.
The height of the wetted wall column required for mass transfer operations is excessive and consequently, this is not widely used, where large quantities of liquid or gas have to be handled, it would be necessary to arrange many vertical pipes in parallel and this leads to difficulties in the distribution of liquid into the inner surface of the tubes. The gas pressure drop for this is confined to skin friction effects, with few or no expansion or contraction losses
.
Mass transfer rates for fluids flowing through pipes have been studied more completely than in other cases.
The rates of diffusion into gases flowing through pipes have been studied in wetted wall columns.
A volatile liquid is submitted to flow down the inside surface of a circular tube, while gas flows upward or downward through the center of the pipe. Measurement of the rate of evaporation of a liquid into the gas stream over a known surface permits calculation of the mass transfer coefficient for the diffusion of vapor into the gas stream. Since the liquid is pure, the concentration gradient for diffusion exists entirely within the gas phase, the mass transfer coefficient Kg may be calculated. Sherwood and Gillard conducted a series of experiments using a variety of volatile liquids with air in a turbulent flow.
Here the mass transfer coefficient in the form of the dimensionless group is plotted against the Reynolds number of the gas for the system air-water (Sc = 60). For gases, values of Re from 2000 to 35,000 were covered and from 0.6 to 2.5 with gas pressures varying from 0.1 to 3 atm.
The equation which describes all the data for both liquid and gas flow is
(KG d/DW (PBM/P) (Kld/D) = 0.023 Re0.83 Sc1/3
This empirical relation is quite remarkable in the manner in which it generally confirms the relationship between heat mass and momentum transfer developed theoretically. However, the evaporation of the volatile liquids in a wetted wall column results in the cooling of the liquids and consequent simultaneous heat transfer between liquid and gas. The heat transfer rates are given by the equation
HD / k = 0.023 Re0.8 Pr0.3
Owing to ripples and waves on the liquid surface.
Interphase Mass Transfer
Equipment used: Wetted Wall column unit, Humidity meter
The material used: Water
EXPERIMENTAL PROCEDURE:
1. Water is fed to the column at a rate at which complete wetting with a minimum of ripple formation is visible.
2. The blower is started and the minimum flow of air is maintained.
3. After about 5 minutes, when steady state condition reaches, the humidity of air at the inlet and outlet are determined by the readings of the wet and dry bulb thermometers and by the use of a psychometric chart.
4. Water flow rates and inlet and outlet temperatures are noted.
5. Vapor pressure of water at different water temperatures is calculated.
6. Calculations are made at different flow rates and values of Kg Vs NRA are plotted on a log-log scale.
OBSERVATIONS:
| S.No | Air flow rate from M2 Qa pm | Water flow rate Qw pm | Air temperature | Water temperature 0C | Air PD mm H20 across the orifice | |
| Inlet | Outlet | T1 T2 | M1 M2 | |||
| Td1tw1 | Td2 tw2 | |||||
| 1 | ||||||
| 2 |
Length of the tube =
Diameter of tube =
From the readings, Td1, tw1 and Td2 , tw2 and from a psychometric chart,
The partial pressure of water vapor at inlet = P1 KN/m2
The partial pressure of water at the outlet = PB KN/m2
DATA ANALYSIS:
Mean air pressure in column Pt = PB *(DP1/2)X1000/13600*1.013*100/760 KN/m2
Air flow rate =
9.22 XSQRTDP2/106 kg moles/sec
Driving force at inlet of air= DpW1 = PW1 –pw1
Where,
pw1 =pure component vapor pressure of water at outlet water temp T1
PW1 = Partial pressure of water at the bottom
Driving force at the outlet of the air
DpW1 = PW2 –pw2
where,
pw1 =pure component vapor pressure of water at outlet water temp T2
PW2= Partial pressure of water at the top of the column
DPwm = (DpW1 – DpW2)/ ln (DpW1/DpW2)
Amount of water evaporated
NW = QA* (pw2/Pt – pw1/Pt)
In terms of mass transfer coefficient Kg, the rate of mass transfer is given by
Nw = KG * A* DPwm
where A = p DL m2 where d = i.d of column and L = Effective length of column
For each flow rate of air, Kg can be calculated.
Pam = (Pt – pw1) – (Pt –Pw2)/ ln (Pt – pw1/ Pt –Pw2) is also calculated
To plot Gillard correlation, Kg * (d/DW)* (Pam/Pt) * (rADw/mair) 0.44
Where Dw = diffusivity of water vapor in air = 0.13X10-4 m2/sec
mair =viscosity of air = 1.85X 10-3 kg/m/sec
Nre = dG/ mair = d.QA.AC/mair
Ac=cross section area of the column
d = diameter of the column
Kg * (d/DW)* (Pam/Pt) * (rADw/mair) 0.44 Vs Are is plotted on a log-log scale.
This value is compared with reported values.
RESULTS:
Reported value =
Calculated value =
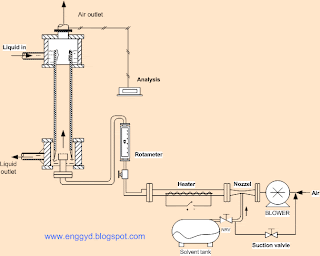
The above setup is used to calculate the experimental mass transfer coefficient of the liquid and gas system at different temperatures and different flow rates; of course, the main application of the wetted walls is to determine the data of the gas and liquid mass transfer coefficient.
The blower is provided with two valves at suction so that when the studies are focused on vapors of chemical substance which are stored in a storage vessel and the vapors from the vessel are sucked by the blower and passed into the column or if the vapors are required to be mixed with air than an option at the discharge line of the blower which is facilitated with nozzle helps in mixing the vapor with air.
A heater is provided at the discharge line to supply heat to the vapor or air to maintain the temperature of the system and the whole pipeline is insulated to prevent the loss, by using the rotameter, the flow rate of the vapor can be controlled.
 |
| PSYCHROMETRIC CHARTS |
Related topic – click here
- MASS TRANSFER EXTRACTION
- Wetted Wall Column Experiment
- Recompression Methods | Forced Circulation Evaporators | Long Vertical Tube Evaporator | Evaporation And Types Of Evaporation Equipment
- Direct Hydration Process Of Ethylene To Produce Synthetic Ethanol
- Power Generator Working And Types Of Power Generators | The World’s Energy Sources
- Mass Transfer Studies On Electrode Support In An Electrolytic Cell
- Electric Lamps And Lighting Calculations, Definitions And Units | Electrical Earthing Or Grounding



