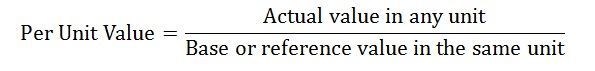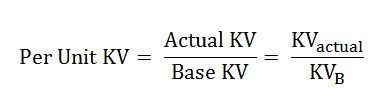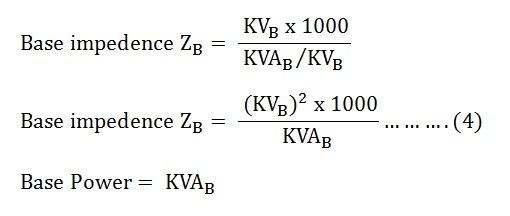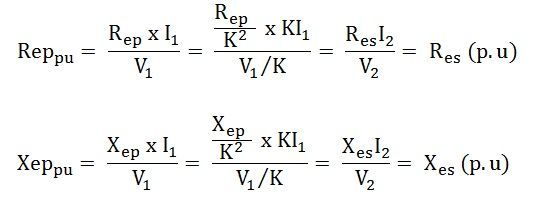What Is A Per Unit System? | Advantages of Per-Unit System in Power System Analysis

THE PER-UNIT SYSTEM

In many engineering situations, it is useful to scale or normalize, dimensioned quantities. This is commonly done in power system analysis. The standard method used is referred to as the per-unit system. Historically, this was done to simplify numerical calculations that were made by hand. Although this advantage is eliminated by the calculator, other advantages remain.

• Device parameters tend to fall into a relatively narrow range, making erroneous values conspicuous.

• Using this method all quantities are expressed as ratios of some base value or values.

• The per-unit equivalent impedance of any transformer is the same when referred to either the primary or the secondary side.

• The per-unit impedance of a transformer in a three-phase system is the same regardless of the type of winding connections (wye-delta, delta-wye, wye-wye, or delta-delta).

• The per-unit method is independent of voltage changes and phase shifts through transformers where the base voltages in the winding are proportional to the number of turns in the windings.

• Manufactures usually specify the impedance of equipment in per-unit or percent on the basis of its nameplate rating of power (usually kVA) and voltage (V or kV). The per-unit system is simply a scaling method. The basic per-unit scaling equation is

Per Unit = Actual Value/ Base Value

The base value always has the same units as the actual value, forcing the per-unit value to be dimensionless. The base value is always a real number, whereas the actual value may be complex. The subscript pu will indicate a per-unit value. The subscript base will indicate a base value, and no subscript will indicate an actual value such as Amperes, Ohms, or Volts.

Per-unit quantities are similar to percent quantities. The ratio in percent is 100 times the ratio per unit. For example, a voltage of 70kV on a base of 100kV would be 70% of the base voltage. This is
equal to 100 times the per unit value of 0.7 derived above.

APPLICATION OF PER-UNIT SYSTEM

Applying this to relay settings, a practical example can be shown in the calculation of the settings for a relay on a transmission line. For distance relays a common setting for zone 1 is 85% of the line impedance. Zone 2 should be set not less than 125% of the line, with care to not overreach zone 1 of the next line section. If this does then zone 2 will need to be coordinated with the next line section zone 2.

Definition: The per-unit value of any quantity is defined as the ratio of the actual value in any unit to the base or reference value in the same unit. Any quantity is converted into per unit quantity by dividing the numeral value by the chosen base value of the same dimension. The per-unit value is dimensionless.

The base values can be selected arbitrarily. It is usual to assume the base values as given below

Base voltage = rated voltage of the machine
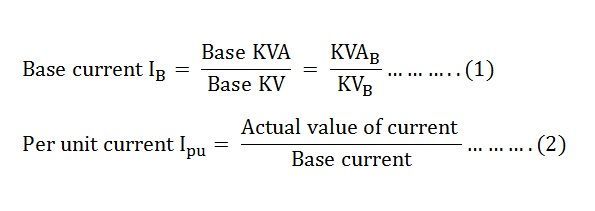
Base current = rated current of the machine
Base impedance = base voltage /base current
Base power = base voltage x base current

Firstly the value of base power and the base voltage is selected, and their choice automatically fixes the other base values.
As
So, Putting the value of base current from equation (1) into equation (2) we get

Putting the value of base current from equation (1) in equation (3) we get

Now,
Putting the value of base impedance from equation (4) in equation (5) we will get the value of impedance per unit

Advantages of Per Unit System

There are two advantages of using the Per Unit System.

The parameters of the rotating electrical machines and the transformer lie roughly in the same range of numerical values, irrespective of their ratings if expressed in a per-unit system of ratings.
It relieves the analyst of the need to refer circuit quantities to one or the other side of the transformer, making the calculations easy.

Taking the example of a transformer having the resistance in the per unit as R_pu ohm and the reactance as X_puin ohm with referred to primary then per unit values will be

Where R_ep and X_ep are resistance and reactance referred to as primary and pu mean in the per-unit system.

The resistance and leakage reactance referred to as primary per unit are the same as those referred to as secondary in the per-unit system because

Where R_es and X_es are the equivalent resistance and reactance referred to as secondary

Therefore, from the above two equations, it is clear that the need for an ideal transformer is eliminated. This is so because the per-unit impedance is the same for the equivalent circuit of the transformer whether computed from the primary or secondary as long as the voltage bases on the two sides are selected in the ratio of transformation.

ADVANTAGES OF PER UNIT SYSTEM

PER UNIT SYSTEM

The per-unit system expressed the voltages, currents, powers, impedances, and other electrical quantities basis by the equation:

Quantity per unit (pu) = Actual value/ Base value of quantity

ADVANTAGES OF PER UNIT SYSTEM

While performing calculations, referring quantities from one side of the transformer to the other side serious errors may be committed. This can be avoided by using a per-unit system.
Voltages, currents, and impedances expressed per unit do not change when they are referred from one side of the transformer to the other side. This is a great advantage.
Per unit impedances of electrical equipment of similar type usually lie within a narrow range, when the equipment ratings are used as base values.
Transformer connections do not affect the per-unit values.
Manufacturers usually specify the impedances of machines and transformers in per unit or percent of nameplate ratings.
Transformers can be replaced by their equivalent series impedances.
Equipment impedances can be easily estimated since their per-unit impedances lie within a relatively narrow range.
Reduced calculations in three-phase systems.
By the choice of voltage bases, the solution of networks containing several transformers is easy.
More useful for digital computation.
For apparatus of the same general type the p.u. and volt drops or losses are in the same order, regardless of size.
For transformers, the p.u. of impedances are the same for the primary and secondary sides.

PER UNIT CONVERSION PROCEDURE OF SINGLE PHASE

Pick a VA base for the entire system, S_base
Pick a voltage base for each different voltage level, V_base.
Voltage bases are related by transformer turns ratios.
Voltages are line to neutral.
Calculate the impedance base, Z_base = (V_base)²/S_base
Calculate the current base, I_base =V_base/Z_base
Convert actual values to per unit
Convert to per unit (p.u.) (many problems are already in per unit)
Solve
Convert back to actual as necessary